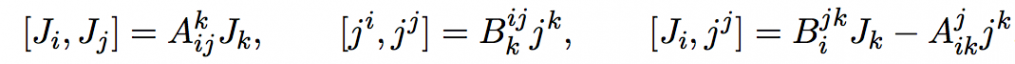In this contribution (arXiv:2212.11750) we present a general procedure that allows the construction of noncommutative spaces with quantum group invariance as the quantization of their associated coisotropic Poisson homogeneous spaces coming from a coboundary Lie bialgebra structure. The approach is illustrated by obtaining in an explicit form several noncommutative spaces from (3+1)D (A)dS and Poincaré coisotropic Lie bialgebras. In particular, we review the construction of the κ-Minkowski and κ-(A)dS spacetimes in terms of the cosmological constant Λ. Furthermore, we present all noncommutative Minkowski and (A)dS spacetimes that preserved a quantum Lorentz subgroup. Finally, it is also shown that the same setting can be used to construct the three possible 6D κ-Poincaré spaces of time-like. Some open problems are also addressed.

The noncommutative spacetimes associated to the κ-Poincaré relativistic symmetries and their “non-relativistic” (Galilei) and “ultra-relativistic” (Carroll) limits are indistinguishable, since their coordinates satisfy the same algebra. In this work (arXiv:2212.01125), we show that the three quantum kinematical models can be differentiated when looking at the associated spaces of time-like worldlines. Specifically, we construct the noncommutative spaces of time-like geodesics with κ-Galilei and κ-Carroll symmetries as contractions of the corresponding κ-Poincaré space and we show that these three spaces are defined by different algebras. In particular, the κ-Galilei space of worldlines resembles the so-called Euclidean Snyder model, while the κ-Carroll space turns out to be commutative. Furthermore, we identify the map between quantum spaces of geodesics and the corresponding noncommutative spacetimes, which requires to extend the space of geodesics by adding the noncommutative time coordinate.

We review (arXiv:2211.11684) the main features of models where relativistic symmetries are deformed at the Planck scale. We cover the motivations and links to other quantum gravity approaches. We describe in some detail the most studied theoretical frameworks, including Hopf algebras, relative locality, and other scenarios with deformed momentum space geometry. We discuss possible phenomenological consequences, and point out current open questions.

In this work (arXiv:2211.11627) we discuss the construction of a free scalar quantum field theory on κ-Minkowski noncommutative spacetime. We do so in terms of κ-Poincaré-invariant N-point functions, i.e. multilocal functions which respect the deformed symmetries of the spacetime. As shown in a previous paper by some of us, this is only possible for a lightlike version of the commutation relations, which allow the construction of a covariant algebra of N points that generalizes the κ-Minkowski commutation relations. We solve the main shortcoming of our previous approach, which prevented the development of a fully covariant quantum field theory: the emergence of a non-Lorentz-invariant boundary of momentum space. To solve this issue, we propose to “extend” momentum space by introducing a class of new Fourier modes and we prove that this approach leads to a consistent definition of the Pauli-Jordan function, which turns out to be undeformed with respect to the commutative case. We finally address the quantization of our scalar field and obtain a deformed, κ-Poincaré-invariant, version of the bosonic oscillator algebra.

Quantum gravity is expected to introduce quantum aspects into the description of reference frames. In this paper (arXiv:2211.11347) we set the stage for exploring how quantum gravity induced deformations of classical symmetries could modify the transformation laws among reference frames in an effective regime. We invoke the quantum group SUq(2) as a description of deformed spatial rotations and interpret states of a representation of its algebra as describing the relative orientation between two reference frames. This leads to a quantization of one of the Euler angles and to the new paradigm of agency-dependence: space is reconstructed as a collection of fuzzy points, exclusive to each agent, which depends on their choice of reference frame. Each agent can choose only one direction in which points can be sharp, while points in all other directions become fuzzy in a way that depends on this choice. Two agents making different choices will thus observe the same points with different degrees of fuzziness.

In this work (arXiv:2210.10111) we consider the effects of Lorentz Invariance Violation over the observed flux of very high-energy neutrinos. For that, we study the neutrino propagation in a Modified Dispersion Relation scenario with a superluminal velocity. This makes the neutrino unstable and causes a cut-off in the flux of detected neutrinos. Using simple models, one can approximate the location of the cut-off as function of the parameters of new physics and the closest source.

In this paper (arXiv:2210.02222), the kinematics of the three body decay, with a modified energy-momentum relation of the particles due to a violation of Lorentz invariance, is presented in detail in the collinear approximation. The results are applied to the decay of superluminal neutrinos producing an electron-positron or a neutrino-antineutrino pair. Explicit expressions for the energy distributions, required for a study of the cascade of neutrinos produced in the propagation of superluminal neutrinos, are derived.

The so-called Darboux III oscillator is an exactly solvable N-dimensional nonlinear oscillator defined on a radially symmetric space with non-constant negative curvature. This oscillator can be interpreted as a smooth (super)integrable deformation of the usual N-dimensional harmonic oscillator in terms of a non-negative parameter λ which is directly related to the curvature of the underlying space. In this paper (arXiv:2209.05293), a detailed study of the Shannon information entropy for the quantum version of the Darboux III oscillator is presented, and the interplay between entropy and curvature is analysed. In particular, analytical results for the Shannon entropy in the position space can be found in the N-dimensional case, and the known results for the quantum states of the N-dimensional harmonic oscillator are recovered in the limit of vanishing curvature λ→0. However, the Fourier transform of the Darboux III wave functions cannot be computed in exact form, thus preventing the analytical study of the information entropy in momentum space. Nevertheless, in the one-dimensional case, we have computed the latter numerically and we find that by increasing the absolute value of the negative curvature (through a larger λ parameter) the information entropy in position space increases, while in momentum space it becomes smaller. This result is indeed consistent with the spreading properties of the wave functions of this quantum nonlinear oscillator, which are explicitly shown.

Noncommutative spaces of geodesics provide an alternative way of introducing noncommutative relativistic kinematics endowed with quantum group symmetry. In this paper (arXiv:2208.05851) we present explicitly the seven noncommutative spaces of time-, space- and light-like geodesics that can be constructed from the time-, space- and light- versions of the κ-Poincaré quantum symmetry in (3+1) dimensions. Remarkably enough, only for the light-like (or null-plane) κ-Poincaré deformation the three types of noncommutative spaces of geodesics can be constructed, while for the time-like and space-like deformations both the quantum time-like and space-like geodesics can be defined, but not the light-like one. This obstruction comes from the constraint imposed by the coisotropy condition for the corresponding deformation with respect to the isotropy subalgebra associated to the given space of geodesics, since all these quantum spaces are constructed as quantizations of the corresponding classical coisotropic Poisson homogeneous spaces. The known quantum space of geodesics on the light cone is given by a five-dimensional homogeneous quadratic algebra, and the six nocommutative spaces of time-like and space-like geodesics are explicitly obtained as six-dimensional nonlinear algebras. Five out of these six spaces are here presented for the first time, and Darboux generators for all of them are found, thus showing that the quantum deformation parameter 1/κ plays exactly the same algebraic role on quantum geodesics as the Planck constant ℏ plays in the usual phase space description of quantum mechanics.