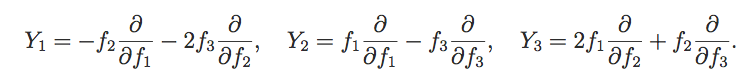Our research is aimed to study different algebraic and geometric techniques based on Lie groups, quantum groups and their representation theory, and to develope their applications in:

• Poisson-Lie groups and Poisson geometry.
• Classical and quantum (super)integrable Hamiltonian systems.
• Lie-Hamilton systems.
• Nonlinear dynamical systems.
• Shape dynamics.
• Relativistic and non-relativistic spacetime geometries.
• Quantum deformations of spacetime symmetries.
• Non-commutative spacetimes and quantum geometry.
• Quantum gravity phenomenology.
• Classical and quantum field theory.
• Quantum reference frames.
• Quantum information theory.
• Quantum computation and quantum communications.