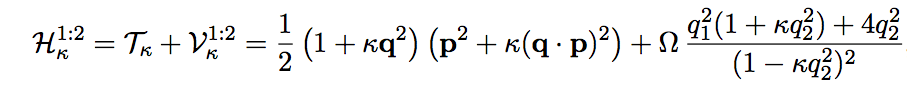In this paper (arXiv:2502.02491) we consider the quantum analog of the generalized Zernike systems. This two-dimensional quantum model, besides the conservation of the angular momentum, exhibits higher-order integrals of motion within the enveloping algebra of the Heisenberg algebra 𝔥2. By constructing suitable combinations of these integrals, we uncover a polynomial Higgs-type symmetry algebra that, through an appropriate change of basis, gives rise to a deformed oscillator algebra. The associated structure function Φ is shown to factorize into two commuting components Φ=Φ1.Φ2. This framework enables an algebraic determination of the possible energy spectra of the model for the cases N=2,3,4, the case N=1 being canonically equivalent to the harmonic oscillator. Based on these findings, we propose two conjectures which generalize the results for all N≥2 and any value of the coefficients of the model, and they are explicitly proven for N=5. In addition, all of these results can be interpreted as superintegrable perturbations of the original quantum Zernike system corresponding to N=2 which are also analyzed and applied to the isotropic oscillator on the sphere, hyperbolic and Euclidean spaces.
Author: angballesteros
Doubly quantum mechanics
Motivated by the expectation that relativistic symmetries might acquire quantum features in Quantum Gravity, in this paper (arXiv:2412.05997) we take the first steps towards a theory of ”Doubly” Quantum Mechanics, a modification of Quantum Mechanics in which the geometrical configurations of physical systems, measurement apparata, and reference frame transformations are themselves quantized and described by ”geometry” states in a Hilbert space. We develop the formalism for spin-1/2 measurements by promoting the group of spatial rotations SU(2) to the quantum group SU_q(2) and generalizing the axioms of Quantum Theory in a covariant way. As a consequence of our axioms, the notion of probability becomes a self-adjoint operator acting on the Hilbert space of geometry states, hence acquiring novel non-classical features. After introducing a suitable class of semi-classical geometry states, which describe near-to-classical geometrical configurations of physical systems, we find that probability measurements are affected, in these configurations, by intrinsic uncertainties stemming from the quantum properties of SU_q(2). This feature translates into an unavoidable fuzziness for observers attempting to align their reference frames by exchanging qubits, even when the number of exchanged qubits approaches infinity, contrary to the standard SU(2) case.
Generalized Buchdahl equations as Lie-Hamilton systems: Quantum deformations and their general solution
In this paper (arXiv:2412.06057) we revisit the nonlinear second-order differential equations x´´(t)=a(x)x´(t)^2+b(t)x´(t), where a(x) and b(t) are arbitrary functions on their argument from the perspective of Lie-Hamilton systems. For the particular choice a(x)=3/x and b(t)=1/t, these equations reduce to the Buchdahl equation considered in the context of General Relativity. It is shown that these equations are associated to the ‘book’ Lie algebra 𝔟2, determining a Lie-Hamilton system for which the corresponding t-dependent Hamiltonian and the general solution of the equations are given. The procedure is illustrated considering several particular cases. We also make use of the quantum deformation of 𝔟2 with quantum deformation parameter z (where q=e^z), leading to a deformed generalized Buchdahl equation. Applying the formalism of Poisson-Hopf deformations of Lie-Hamilton systems, we derive the corresponding deformed t-dependent Hamiltonian, as well as its general solution. The presence of the quantum deformation parameter z is interpreted as the introduction of an integrable perturbation of the initial generalized Buchdahl equation, which is described in detail in its linear approximation.
Mechanical presymplectic structures and Marsden-Weinstein reduction of time-dependent Hamiltonian systems
In 1986, Albert proposed a Marsden-Weinstein reduction process for cosymplectic structures. In this paper (arXiv:2411.11997), we present the limitations of this theory in the application of the reduction of symmetric time-dependent Hamiltonian systems. As a consequence, we conclude that cosymplectic geometry is not appropriate for this reduction. Motived for this fact, we replace cosymplectic structures by more general structures: mechanical presymplectic structures. Then, we develop Marsden-Weinstein reduction for this kind of structures and we apply this theory to interesting examples of time-dependent Hamiltonian systems for which Albert’s reduction method doesn’t work.
Lie-Hamilton systems associated with the symplectic Lie algebra 𝔰𝔭(6,ℝ)
In this paper (arXiv:2409.18489), new classes of Lie-Hamilton systems are obtained from the six-dimensional fundamental representation of the symplectic Lie algebra 𝔰𝔭(6,ℝ). The ansatz is based on a recently proposed procedure for constructing higher-dimensional Lie-Hamilton systems through the representation theory of Lie algebras. As applications of the procedure, we study a time-dependent electromagnetic field and several types of coupled oscillators. The irreducible embedding of the special unitary Lie algebra 𝔰𝔲(3) into 𝔰𝔭(6,ℝ) is also considered, yielding Lie-Hamilton systems arising from the sum of the quark and antiquark three-dimensional representations of 𝔰𝔲(3), which are applied in the construction of t-dependent coupled systems. In addition, t-independent constants of the motion are obtained explicitly for all these Lie-Hamilton systems, which allows the derivation of a nonlinear superposition rule
Lie-Hamilton systems on Riemannian and Lorentzian spaces from conformal transformations and some of their applications
In this paper (arXiv:2407.01500), we propose a generalization of two classes of Lie-Hamilton systems on the Euclidean plane to two-dimensional curved spaces, leading to novel Lie-Hamilton systems on Riemannian spaces (flat 2-torus, product of hyperbolic lines, sphere and hyperbolic plane), pseudo-Riemannian spaces (anti-de Sitter, de Sitter, and Minkowski spacetimes), as well as to semi-Riemannian spaces (Newtonian or non-relativistic spacetimes). The vector fields, Hamiltonian functions, symplectic form and constants of the motion of the Euclidean classes are recovered by a contraction process. The construction is based on the structure of certain subalgebras of the so-called conformal algebras of the two-dimensional Cayley-Klein spaces. These curved Lie-Hamilton classes allow us to generalize naturally the Riccati, Kummer-Schwarz and Ermakov equations on the Euclidean plane to curved spaces, covering both the Riemannian and Lorentzian possibilities, and where the curvature can be considered as an integrable deformation parameter of the initial Euclidean system.
Unimodularity and invariant volume forms for Hamiltonian dynamics on coisotropic Poisson homogeneous spaces
In this paper (arXiv:2408.14091), we introduce the notion of a multiplicative unimodularity for a coisotropic Poisson homogeneous space. Then, we discuss the unimodularity and the multiplicative unimodularity for these spaces and the existence of an invariant volume form for explicit Hamiltonian systems on such spaces. Several interesting examples illustrating the theoretical results are also presented.
Generalized Hamilton spaces: new developments and applications
In this work (arXiv:2407.18819), we make new developments in generic cotangent bundle geometries, depending on all phase-space variables. In particular, we will focus on the so-called generalized Hamilton spaces, discussing how the main ingredients of this geometrical framework, such as the Hamiltonian and the nonlinear and affine connections, can be derived from a given metric. Several properties of this kind of spaces are demonstrated for autoparallel Hamiltonians. Moreover, we study the spacetime and momentum isometries of the metric. Finally, we discuss the possible applications of cotangent bundle geometries in quantum gravity, such as the construction of deformed relativistic kinematics and non-commutative spacetimes.
A physical reinterpretation of heat capacity discontinuities for static black holes
A generic characteristic of self-graviting systems is that they have a negative heat capacity. An important example of this behaviour is given by the Schwarzschild black hole. The case of charged and rotating black holes is even more interesting, since a change of sign of the specific heat takes place through an infinite discontinuity. This has been usually associated with a black hole thermodynamic phase transition appearing at the points where the heat capacity diverges, the so-called Davies points. This aspect of black hole thermodynamics has been addressed from different perspectives, motivating different interpretations since its discovery in the 1970s. In this paper (arXiv:2407.10885), a physical reinterpretation of the heat capacity is provided for spherically symmetric and static black holes. Our analysis is partially based on a reformulation of the black hole heat capacity using the Newman–Penrose formalism. The application to the Reissner-Nordström-de Sitter black hole case reveals a clear physical interpretation of the Newman-Penrose scalars evaluated at the event horizon. This allows us to write the heat capacity as a balance of pressures defined at the horizon. In particular, a matter pressure (coming from the energy-momentum tensor) and a thermal pressure (coming from the holographic energy equipartition of the horizon). The Davies point is identified with the point where the Komar thermal energy density matches the matter pressure at the horizon. We also compare the black hole case with the case of self-graviting objects and their corresponding thermal evolutions. We conclude that the heat capacity of black holes and self-graviting systems can be understood qualitatively in similar terms.
Noncommutative Lightcones from Quantum SO(2,1) Conformal Groups
In this paper (arXiv:2407.12459), five new families of noncommutative lightcones in 2+1 dimensions are presented as the quantizations of the inequivalent Poisson homogeneous structures that emerge when the lightcone is constructed as a homogeneous space of the SO(2,1) conformal group. Each of these noncommutative lightcones maintains covariance under the action of the respective quantum deformation of the SO(2,1) conformal group. We discuss the role played by SO(2,1) automorphisms in the classification of inequivalent Poisson homogeneous lightcones, as well as the geometric aspects of this construction. The localization properties of the novel quantum lightcones are analyzed and shown to be deeply connected with the geometric features of the Poisson homogeneous spaces.