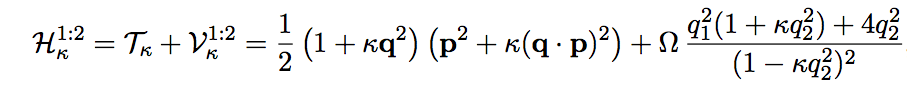In this paper (arXiv:2407.01500), we propose a generalization of two classes of Lie-Hamilton systems on the Euclidean plane to two-dimensional curved spaces, leading to novel Lie-Hamilton systems on Riemannian spaces (flat 2-torus, product of hyperbolic lines, sphere and hyperbolic plane), pseudo-Riemannian spaces (anti-de Sitter, de Sitter, and Minkowski spacetimes), as well as to semi-Riemannian spaces (Newtonian or non-relativistic spacetimes). The vector fields, Hamiltonian functions, symplectic form and constants of the motion of the Euclidean classes are recovered by a contraction process. The construction is based on the structure of certain subalgebras of the so-called conformal algebras of the two-dimensional Cayley-Klein spaces. These curved Lie-Hamilton classes allow us to generalize naturally the Riccati, Kummer-Schwarz and Ermakov equations on the Euclidean plane to curved spaces, covering both the Riemannian and Lorentzian possibilities, and where the curvature can be considered as an integrable deformation parameter of the initial Euclidean system.

In this paper (arXiv:2408.14091), we introduce the notion of a multiplicative unimodularity for a coisotropic Poisson homogeneous space. Then, we discuss the unimodularity and the multiplicative unimodularity for these spaces and the existence of an invariant volume form for explicit Hamiltonian systems on such spaces. Several interesting examples illustrating the theoretical results are also presented.

In this work (arXiv:2407.18819), we make new developments in generic cotangent bundle geometries, depending on all phase-space variables. In particular, we will focus on the so-called generalized Hamilton spaces, discussing how the main ingredients of this geometrical framework, such as the Hamiltonian and the nonlinear and affine connections, can be derived from a given metric. Several properties of this kind of spaces are demonstrated for autoparallel Hamiltonians. Moreover, we study the spacetime and momentum isometries of the metric. Finally, we discuss the possible applications of cotangent bundle geometries in quantum gravity, such as the construction of deformed relativistic kinematics and non-commutative spacetimes.

A generic characteristic of self-graviting systems is that they have a negative heat capacity. An important example of this behaviour is given by the Schwarzschild black hole. The case of charged and rotating black holes is even more interesting, since a change of sign of the specific heat takes place through an infinite discontinuity. This has been usually associated with a black hole thermodynamic phase transition appearing at the points where the heat capacity diverges, the so-called Davies points. This aspect of black hole thermodynamics has been addressed from different perspectives, motivating different interpretations since its discovery in the 1970s. In this paper (arXiv:2407.10885), a physical reinterpretation of the heat capacity is provided for spherically symmetric and static black holes. Our analysis is partially based on a reformulation of the black hole heat capacity using the Newman–Penrose formalism. The application to the Reissner-Nordström-de Sitter black hole case reveals a clear physical interpretation of the Newman-Penrose scalars evaluated at the event horizon. This allows us to write the heat capacity as a balance of pressures defined at the horizon. In particular, a matter pressure (coming from the energy-momentum tensor) and a thermal pressure (coming from the holographic energy equipartition of the horizon). The Davies point is identified with the point where the Komar thermal energy density matches the matter pressure at the horizon. We also compare the black hole case with the case of self-graviting objects and their corresponding thermal evolutions. We conclude that the heat capacity of black holes and self-graviting systems can be understood qualitatively in similar terms.

In this paper (arXiv:2407.12459), five new families of noncommutative lightcones in 2+1 dimensions are presented as the quantizations of the inequivalent Poisson homogeneous structures that emerge when the lightcone is constructed as a homogeneous space of the SO(2,1) conformal group. Each of these noncommutative lightcones maintains covariance under the action of the respective quantum deformation of the SO(2,1) conformal group. We discuss the role played by SO(2,1) automorphisms in the classification of inequivalent Poisson homogeneous lightcones, as well as the geometric aspects of this construction. The localization properties of the novel quantum lightcones are analyzed and shown to be deeply connected with the geometric features of the Poisson homogeneous spaces.

These notes (arXiv:2311.01911) cover part of the lectures presented by Andrea Maselli for the 59th Winter School of Theoretical Physics and third COST Action CA18108 Training School ‘Gravity — Classical, Quantum and Phenomenology’. The school took place at Palac Wojanów, Poland, from February 12th to 21st, 2023. The lectures focused on some key aspects of black hole physics, and in particular on the dynamics of particles and on the scattering of waves in the Schwarzschild spacetime. The goal of the course was to introduce the students to the concept of black hole quasi normal modes, to discuss their properties, their connection with the geodesic motion of massless particles, and to provide numerical approaches to compute their actual values.

In this paper (arXiv:2406.17479) a new procedure for the construction of higher-dimensional Lie-Hamilton systems is proposed. This method is based on techniques belonging to the representation theory of Lie algebras and their realization by vector fields. The notion of intrinsic Lie-Hamilton system is defined, and a sufficiency criterion for this property given. Novel four-dimensional Lie-Hamilton systems arising from the fundamental representation of the symplectic Lie algebra 𝔰𝔭(4,ℝ) are obtained and proved to be intrinsic. Two distinguished subalgebras, the two-photon Lie algebra 𝔥6 and the Lorentz Lie algebra 𝔰𝔬(1,3), are also considered in detail. As applications, coupled time-dependent systems which generalize the Bateman oscillator and the one-dimensional Caldirola-Kanai models are constructed, as well as systems depending on a time-dependent electromagnetic field and generalized coupled oscillators. A superposition rule for these systems, exhibiting interesting symmetry properties, is obtained using the coalgebra method.

This paper (arXiv:2404.08729) is the second part of a series that develops the mathematical framework necessary for studying field theories on “T-Minkowski” noncommutative spacetimes. These spacetimes constitute a class of noncommutative geometries, introduced in Part I, that are each invariant under distinct quantum group deformations of the Poincaré group. All these noncommutative geometries possess certain physically desirable characteristics, which allow me to develop all the tools of differential geometry and functional analysis, that are necessary in order to build consistent and T-Poincaré invariant noncommutative classical field theories.

In this paper (arXiv:2404.01073), integrable deformations of a class of Rikitake dynamical systems are constructed by deforming their underlying Lie-Poisson Hamiltonian structures as linearizations of Poisson–Lie structures on certain (dual) Lie groups. By taking into account that there exists a one-to one correspondence between Poisson–Lie groups and Lie bialgebra structures, a number of deformed Poisson coalgebras can be obtained, which allow the construction of integrable deformations of coupled Rikitake systems. Moreover, the integrals of the motion for coupled systems can be explicitly obtained by means of the deformed coproduct map. The same procedure can be also applied when the initial system is bi-Hamiltonian with respect to two different Lie-Poisson algebras. In this case, to preserve a bi-Hamiltonian structure under deformation, a common Lie bialgebra structure for the two Lie-Poisson structures has to be found. Coupled dynamical systems arising from this bi-Hamiltonian deformation scheme are also presented, and the use of collective `cluster variables’, turns out to be enlightening in order to analyse their dynamical behaviour. As a general feature, the approach here presented provides a novel connection between Lie bialgebras and integrable dynamical systems.