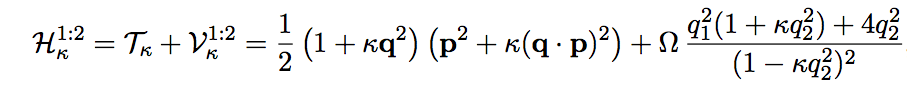The unification of quantum mechanics and general relativity has long been elusive. Only recently have empirical predictions of various possible theories of quantum gravity been put to test. The dawn of multi-messenger high-energy astrophysics has been tremendously beneficial, as it allows us to study particles with much higher energies and travelling much longer distances than possible in terrestrial experiments, but more progress is needed on several fronts.
A thorough appraisal of current strategies and experimental frameworks, regarding quantum gravity phenomenology, is provided here (arXiv:2312.00409). Our aim is twofold: a description of tentative multimessenger explorations, plus a focus on future detection experiments.
As the outlook of the network of researchers that formed through the COST Action CA18108 “Quantum gravity phenomenology in the multi-messenger approach (QG-MM)”, in this work we give an overview of the desiderata that future theoretical frameworks, observational facilities, and data-sharing policies should satisfy in order to advance the cause of quantum gravity phenomenology.

This paper (arXiv:2311.16249) introduces and investigates a class of noncommutative spacetimes that I will call “T-Minkowski,” whose quantum Poincaré group of isometries exhibits unique and physically motivated characteristics. Notably, the coordinates on the Lorentz subgroup remain commutative, while the deformation is confined to the translations (hence the T in the name), which act like an integrable set of vector fields on the Lorentz group. This is similar to Majid’s bicrossproduct construction, although my approach allows the description of spacetimes with commutators that include a constant matrix as well as terms that are linear in the coordinates (the resulting structure is that of a centrally-extended Lie algebra). Moreover, I require that one can define a covariant braided tensor product representation of the quantum Poincaré group, describing the algebra of N-points. This also implies that a 4-dimensional bicovariant differential calculus exists on the noncommutative spacetime. The resulting models can all be described in terms of a numerical triangular R-matrix through RTT relations (as well as RXX, RXY and RXdX relations for the homogeneous spacetime, the braiding and the differential calculus). The R-matrices I find are in one-to-one correspondence with the triangular r-matrices on the Poincaré group without quadratic terms in the Lorentz generators. These have been classified, up to automorphisms, by Zakrzewski, and amount to 16 inequivalent models. This paper is the first of two, focusing on the identification of all the quantum Poincaré groups that are allowed by my assumptions, as well as the associated quantum homogeneous spacetimes, differential calculi and braiding constructions.

In this study (arXiv:2310.15063), we construct a 1+1-dimensional, relativistic, free, complex scalar Quantum Field Theory on a noncommutative spacetime characterized by Lie algebra-type commutators, namely, the lightlike version of κ-Minkowski. The associated κ-Poincaré quantum group of isometries is quasitriangular, and its quantum R matrix facilitates the definition of a braided algebra of N points that retains Poincaré invariance. Leveraging our recent findings, we can now represent the generators of the deformed oscillator algebra as nonlinear redefinitions of undeformed oscillators, which are nonlocal in momentum space. In this representation, the momentum, boost, and charge conjugation operators remain undeformed. The deformation is confined to the creation and annihilation operators. However, this deformation only manifests at the multiparticle level, as the one particle (and antiparticle) states are identical to the undeformed ones. We successfully introduce a covariant, involutive deformed flip operator using the R matrix. The corresponding deformed (anti-)symmetrization operators are covariant and idempotent. We conclude by noticing that P and T are not symmetries of the theory, although PT (and hence CPT) is.

The aim of this paper (arXiv:2310.14123) is twofold. First, we show that when two (or more) different quantum groups share the same noncommutative spacetime, such an ‘ambiguity’ can be resolved by considering together their corresponding noncommutative spaces of geodesics. In any case, the latter play a mathematical/physical role by themselves and, in some cases, they can be interpreted as deformed phase spaces. Second, we explicitly show that noncommutative spacetimes can be reproduced from ‘extended’ noncommutative spaces of geodesics which are those enlarged by the time translation generator. These general ideas are described in detail for the κ-Poincaré and κ-Galilei algebras.

The recent and continuous research on graphene-based systems has opened their usage to a wide range of applications due to their exotic properties. In this paper, we have studied the effects of an electric field on curved graphene nanoflakes, employing the Density Functional Theory. Both mechanical and electronic analyses of the system have been made through its curvature energy, dipolar moment, and quantum regeneration times, with the intensity and direction of a perpendicular electric field and flake curvature as parameters. A stabilisation of non-planar geometries has been observed, as well as opposite behaviours for both classical and revival times with respect to the direction of the external field. Our results show that it is possible to modify regeneration times using curvature and electric fields at the same time. This fine control in regeneration times could allow for the study of new phenomena on graphene.

In this paper (arXiv:2310.02688), the theory of Lie-Hamilton systems is used to construct generalized time-dependent SIS epidemic Hamiltonians with a variable infection rate from the ‘book’ Lie algebra. Although these are characterized by a set of non-autonomous nonlinear and coupled differential equations, their corresponding exact solution is explicitly found. Moreover, the quantum deformation of the book algebra is also considered, from which the corresponding deformed SIS Hamiltonians are obtained and interpreted as perturbations in terms of the quantum deformation parameter of previously known SIS systems. The exact solutions for these deformed systems are also obtained.

These are lecture notes (arXiv:2309.17369) for an introductory course on noncommutative field and gauge theory. We begin by reviewing quantum mechanics as the prototypical noncommutative theory, as well as the geometrical language of standard gauge theory. Then, we review a specific approach to noncommutative field and gauge theory, which relies on the introduction of a derivations-based differential calculus. We focus on the cases of constant and linear noncommutativity, e.g., the Moyal spacetime and the so-called ℝ3λ, respectively. In particular, we review the gφ4 scalar field theory and the U(1) gauge theory on such noncommutative spaces. Finally, we discuss noncommutative spacetime symmetries from both the observer and particle point of view. In this context, the twist approach is reviewed and the λ-Minkowski gφ4 model is discussed.

In this work (arXiv:2309.15305), PT-symmetric Hamiltonians defined on quantum sl(2,ℝ) algebras are presented. We study the spectrum of a family of non-Hermitian Hamiltonians written in terms of the generators of the non-standard Uz(sl(2,ℝ)) Hopf algebra deformation of sl(2,ℝ). By making use of a particular boson representation of the generators of Uz(sl(2,ℝ)), both the co-product and the commutation relations of the quantum algebra are shown to be invariant under the PT-transformation. In terms of these operators, we construct several finite dimensional PT-symmetry Hamiltonians, whose spectrum is analytically obtained for any arbitrary dimension. In particular, we show the appearance of Exceptional Points in the space of model parameters and we discuss the behaviour of the spectrum both in the exact PT-symmetry and the broken PT-symmetry dynamical phases. As an application, we show that this non-standard quantum algebra can be used to define an effective model Hamiltonian describing accurately the experimental spectra of three-electron hybrid qubits based on asymmetric double quantum dots. Remarkably enough, in this effective model, the deformation parameter z has to be identified with the detuning parameter of the system.

Pointlike systems coupled to quantum fields are often employed as toy models for measurements in quantum field theory. In this paper (arXiv:2308.14718), we identify the field observables recorded by such models. We show that in models that work in the strong coupling regime, the apparatus is correlated with smeared field amplitudes, while in models that work in weak coupling the apparatus records particle aspects of the field, such as the existence of a particle-like time of arrival and resonant absorption. Then, we develop an improved field-detector interaction model, adapting the formalism of Quantum Brownian motion, that is exactly solvable. This model confirms the association of field and particle properties in the strong and weak coupling regimes, respectively. Further, it can also describe the intermediate regime, in which the field-particle characteristics `merge’. In contrast to standard perturbation techniques, this model also recovers the relativistic Breit-Wigner resonant behavior in the weak coupling regime. The modulation of field-particle-duality by a single tunable parameter is a novel feature that is, in principle, experimentally accessible.

In this paper (arXiv:2305.02281), the spectrum of bound and scattering states of the one dimensional Dirac Hamiltonian describing fermions distorted by a static background built from two Dirac delta potentials is studied. A distinction will be made between mass-spike and electrostatic Dirac delta-potentials. The second quantisation is then performed to promote the relativistic quantum mechanical problem to a relativistic quantum field theory and study the quantum vacuum interaction energy for fermions confined between opaque plates. The work presented here is a continuation of [Guilarte et al 2019 Front. Phys. 7 109].