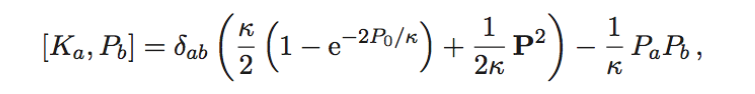The Lie-Hamilton approach for t-dependent Hamiltonians is extended to cover the so-called nonlinear Lie-Hamilton systems (arXiv:2505.13853), which are no longer related to a linear t-dependent combination of a basis of a finite-dimensional Lie algebra of functions W, but an arbitrary t-dependent function on W. This novel formalism is accomplished through a detailed analysis of related structures, such as momentum maps and generalized distributions, together with the extension of the Poisson coalgebra method to a t-dependent frame, in order to systematize the construction of constants of the motion for nonlinear systems. Several relevant relations between nonlinear Lie-Hamilton systems, Lie-Hamilton systems, and collective Hamiltonians are analyzed. The new notions and tools are illustrated with the study of the harmonic oscillator, Hénon-Heiles systems and Painlevé trascendents within a t-dependent framework. In addition, the formalism is carefully applied to construct oscillators with a t-dependent frequency and Kepler-Coulomb systems with a t-dependent coupling constant on the n-dimensional sphere, Euclidean and hyperbolic spaces, as well as on some spaces of non-constant curvature.