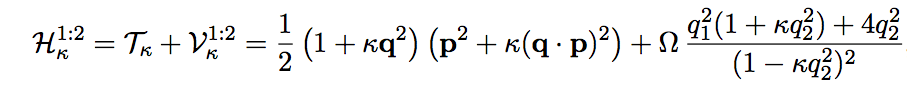In this work (arXiv:2504.21833), we introduce a PT-symmetric infinite-dimensional representation of the U_z(sl(2,R)) Hopf algebra, and we analyse a multiparametric family of Hamiltonians constructed from such representation of the generators of this non-standard quantum algebra. It is shown that all these Hamiltonians can be mapped to equivalent systems endowed with a position-dependent mass. From the latter presentation, it is shown how appropriate point canonical transformations can be further defined in order to transform them into Hamiltonians with constant mass over suitable domains. By following this approach, the bound-state spectrum and the corresponding eigenfunctions of the initial PT-symmetric Hamiltonians can be determined. It is worth stressing that a relevant feature of some of the new U_z(sl(2,R)) systems here presented is found to be their connection with double-well and Pöschl-Teller potentials. In fact, as an application we present a particular Hamiltonian that can be expressed as an effective double-well trigonometric potential, which is commonly used to model several relevant systems in molecular physics.
- Comment
- Reblog
-
Subscribe
Subscribed
Already have a WordPress.com account? Log in now.