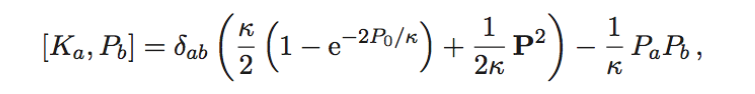In this paper (arXiv:2502.02491) we consider the quantum analog of the generalized Zernike systems. This two-dimensional quantum model, besides the conservation of the angular momentum, exhibits higher-order integrals of motion within the enveloping algebra of the Heisenberg algebra 𝔥2. By constructing suitable combinations of these integrals, we uncover a polynomial Higgs-type symmetry algebra that, through an appropriate change of basis, gives rise to a deformed oscillator algebra. The associated structure function Φ is shown to factorize into two commuting components Φ=Φ1.Φ2. This framework enables an algebraic determination of the possible energy spectra of the model for the cases N=2,3,4, the case N=1 being canonically equivalent to the harmonic oscillator. Based on these findings, we propose two conjectures which generalize the results for all N≥2 and any value of the coefficients of the model, and they are explicitly proven for N=5. In addition, all of these results can be interpreted as superintegrable perturbations of the original quantum Zernike system corresponding to N=2 which are also analyzed and applied to the isotropic oscillator on the sphere, hyperbolic and Euclidean spaces.
- Comment
- Reblog
-
Subscribe
Subscribed
Already have a WordPress.com account? Log in now.