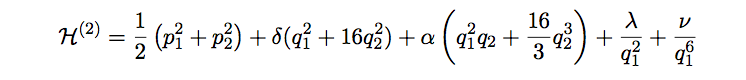In this paper (arXiv:2409.18489), new classes of Lie-Hamilton systems are obtained from the six-dimensional fundamental representation of the symplectic Lie algebra 𝔰𝔭(6,ℝ). The ansatz is based on a recently proposed procedure for constructing higher-dimensional Lie-Hamilton systems through the representation theory of Lie algebras. As applications of the procedure, we study a time-dependent electromagnetic field and several types of coupled oscillators. The irreducible embedding of the special unitary Lie algebra 𝔰𝔲(3) into 𝔰𝔭(6,ℝ) is also considered, yielding Lie-Hamilton systems arising from the sum of the quark and antiquark three-dimensional representations of 𝔰𝔲(3), which are applied in the construction of t-dependent coupled systems. In addition, t-independent constants of the motion are obtained explicitly for all these Lie-Hamilton systems, which allows the derivation of a nonlinear superposition rule